回路図(2)
さて、今回は(2)です。\(Y\)方向の運動について説明します。
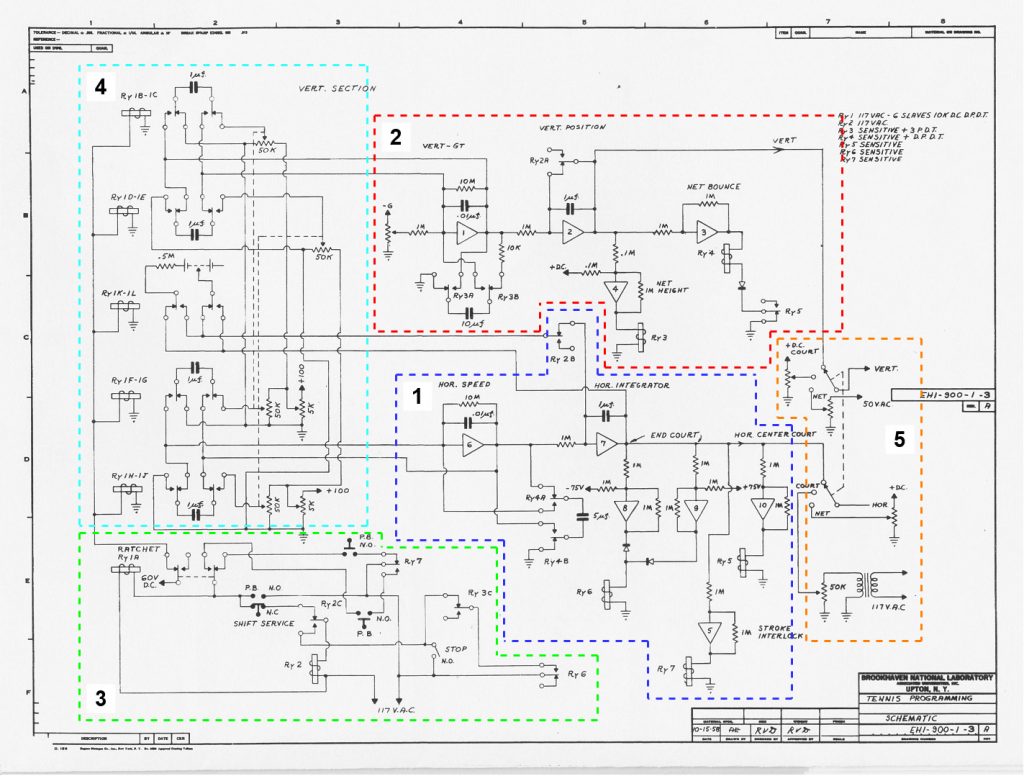
\(X\)方向の運動と同様に運動方程式を考えます。
ボールの運動\(Y\)方向
このゲームのボールは放物線運動をベースにしているので、\(y\)方向の運動方程式は次式となります。
$$m\frac{d^2y}{dt^2}=-mg$$
\(m, g\)はボールの質量と重力加速度です。ただの自由落下と変わりません。位置に関する積分方程式に変換します。ただし、初速は打ち返す角度を\( \theta \)として\(v_{0y} = v_0 \sin{\theta}\)とします。
$$v_y = -\int_0^{T} g dt + v_{0y}$$
$$y = \int_0^{T} \left[ -\int_0^{T} g dt + v_{0y} \right] dt + y_0$$
\( y_0 \)は初期位置です。当たり前ですが、非常にシンプルな式になりましたね。上記の式から積分器は2つ必要なことがわかります。また、重力加速度をマイナス1倍して積分した後に初速\(v_{0y} \)から再度積分すれば、ボールの\(y\)位置がわかることがわかりました。
コートのバウンド
次にコートのバウンドを考えます。当たり前ですが、ネットでのバウンドとほとんど同じ考え方に基づいて式を導出できます。コートでのバウンドでは衝突時のエネルギー損失を考慮に入れます。したがって、真下に落としても落とした高さと同じ高さまでバウンドしません。1ネットでのバウンドと同様に考えて、衝突後の位置は次式で計算できます。
$$y^{hit} = -e\int_0^{T} \mathrm{sgn}(V_y) \ dt + Y_0$$
何やら新しい記号が追加されています。\(e\)は反発係数です。\(0\le e \le 1\)をとります。1のとき完全に反発するのでエネルギー損失がありません。一方、0のときエネルギーがすべて吸収されたことになります。\(e\)を\(0<e<1\)の範囲で選べばエネルギーを消耗しながらバウンドする\(Y\)軌道を再現できます。
回路への落とし込み(ボール位置計算)
回路への落とし込みを考えます。\(X\)方向と全く同じです。違いとしては重力加速度を入力する点です。
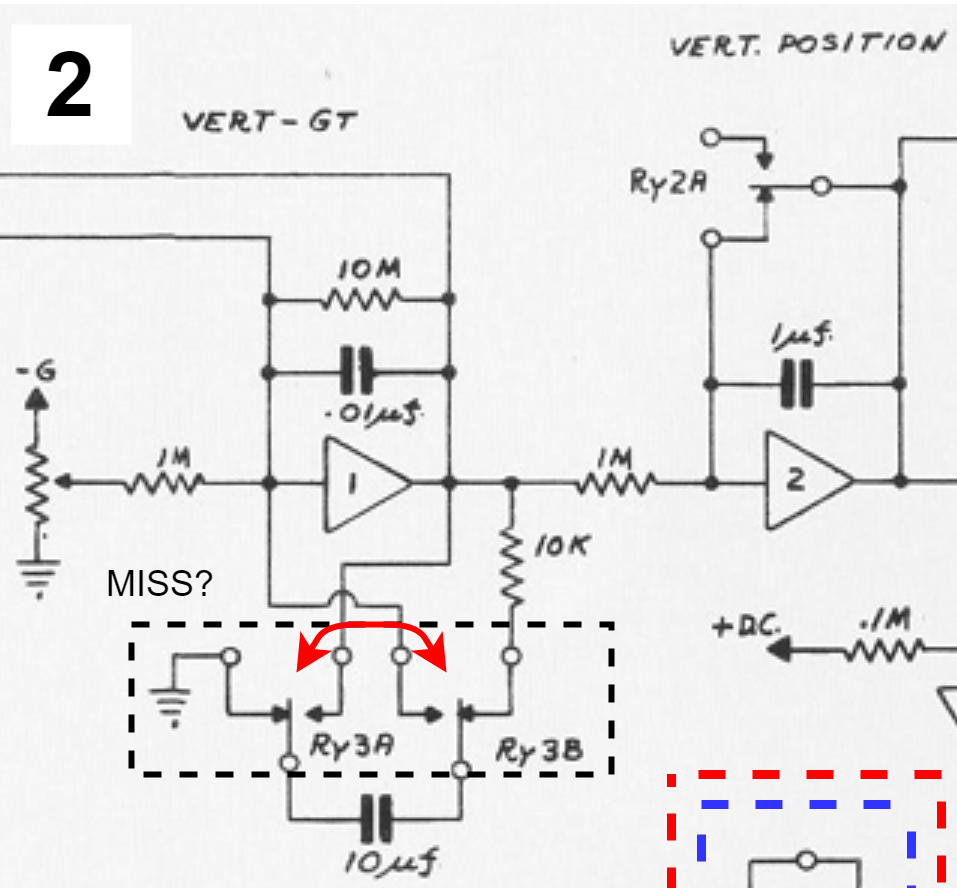
初段のアンプに重力加速度を入力する回路がついていますね。可変抵抗によって重力加速度の大きさを可変としているようです。下側に何やら容量の大きいコンデンサがついています。これはバウンド用ですが、後程説明することにしましょう。
後段は単純な積分器として動作しています。
回路への落とし込み(コートのバウンド)
コートの位置は\(V_{YC}\)で表していますから、ボールの\(y\)位置を表す電圧\(V_y\)に対して次の関係が成立したときにコートに衝突したと考えればよさそうです。
$$V_y \le V_{YC}$$
これを実現するためには加算回路を用います。
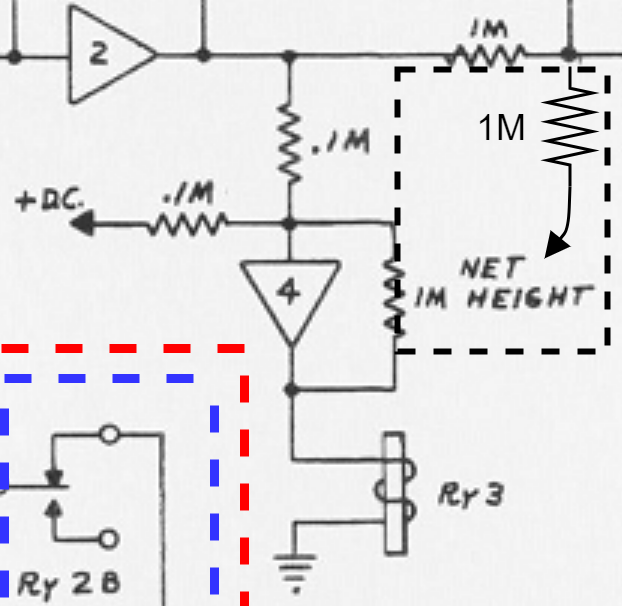
この回路はコート端を検出する回路とほとんど同じです。ただし、増幅率が10倍に設定されています。したがって、ボールのy座標を表す電圧\(V_y\), コートのy位置を表す電圧を\(V_{yc}\)とするとアンプの出力電圧を表す式は次のようになります。
$$V_{out}=-10(V_y + V_{yc})$$
上記の式から\(V_y = -V_{yc}\)付近では出力電圧が0Vになり、RY3がOFFになることがわかります。210倍に増幅している理由はリレーの駆動電圧には数V必要なので、感度を高めるためと思われます。
RY3の接点先を確認すると、10uFのコンデンサ接続が切り替わることがわかります。ただし、この接続はミスだと思われます。アクティブ時の接続とノーマリー時の接続が入れ替わっています。接続が入れ替わっていることを考慮にいれると、衝突時には10uFのコンデンサと1uFのコンデンサが並列に接続されます。では、10uFのコンデンサ電圧はどのようになっているのでしょうか?
10uFのコンデンサには10kΩを介して、y方向のボール速度\(v_y\)を表す電圧により充放電が行われています。この10kΩが味噌です。10uFのコンデンサ電圧を\(V_{C}\)、抵抗値を\(R\)とすると、y方向のボール速度\(v_y\)との関係を求めます。ラプラス変換を用いて導出します。初期値を0として、ステップ的に電圧が与えらえたとします。
$$ V_C = \mathfrak{L}^-1 \left[ \frac{1}{RC} \cdot \frac{1}{s + \frac{1}{RC}} \cdot -\frac{g}{s} \cdot \frac{1}{s} \right] $$
として計算できます。部分分数分解を利用して解くと、
$$ V_C = \mathfrak{L}^-1 \left[ \frac{1}{RC} \cdot \frac{-g}{s^2(s + \frac{1}{RC})} \right] $$
$$ V_C = \mathfrak{L}^-1 \left[ \frac{-g}{RC} \cdot \left( \frac{(RC)^2}{s^2} – \frac{RC}{s} + \frac{(RC)^2}{(s + \frac{1}{RC})} \right) \right] $$
$$ V_C = -g \left[ RCt – 1 + RCe^{-\frac{t}{RC}} \right] $$
$$ V_C = -g \left[ RC(t+e^{-\frac{t}{RC}}) – 1 \right] $$
\(RC=1, g=1\)とすると、時間応答は次のグラフになります。
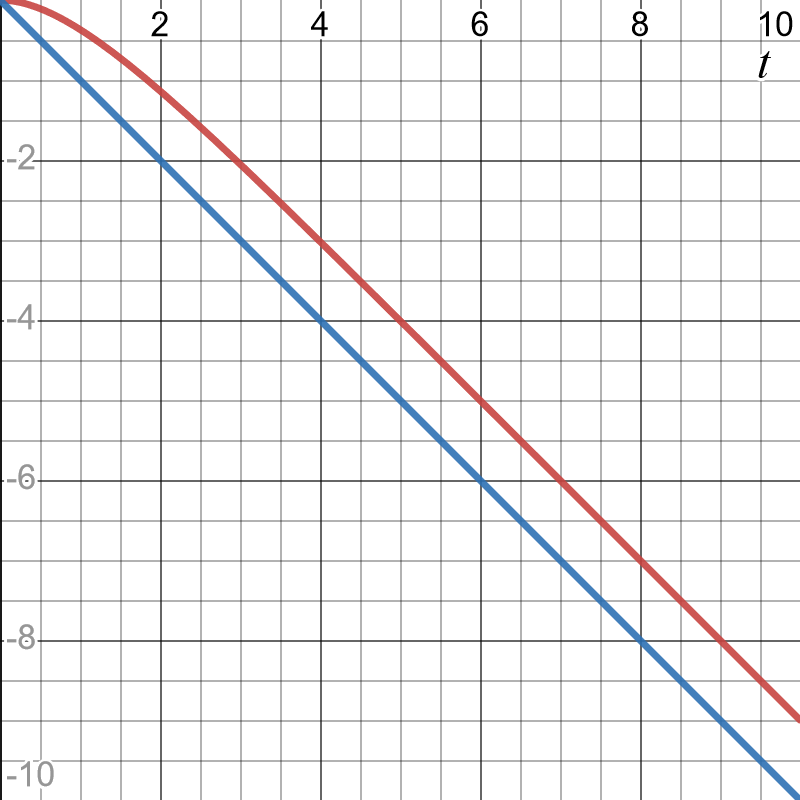
青はボールの落下速度、赤は速度保持用の10uFのコンデンサの電圧\(V_C\)です。このよう常に定常偏差が発生します。この時、赤と青の定常偏差を求めてみます。
$$e_t = \left( -gt + g \left[ RC(t+e^{-\frac{t}{RC}}) – 1 \right] \right)$$
\(e^{-\frac{t}{RC}}\)は0に収束するので、tが十分に大きければ、
$$e_t => gt\left( RC – 1 \right)-g$$
が成り立ちます。RC=1とすると、\(e_t=-g\)となり先ほどのグラフに一致します。
初段の積分器に用いられているコンデンサの容量は1uFですが、速度保持用のコンデンサは10uFです。衝突時に1uFと10uFのコンデンサが並列となりますが、圧倒的に10uFのほうが支配的です。並列に接続された時の電圧\(V\)は次式です。
$$V = \frac{C_1 V_1 + C_2 V_2}{C_1 + C_2}$$
\(C_1 = 1uF, C_2 = 10uF, V_1 = V_y, V_2 = V_C\)とすると、
$$V = \frac{V_y + 10 V_C}{11} = \frac{V_y}{11} + 10\frac{V_C}{11}$$
$$V \approx V_C$$
したがって、リレーが動作しときには瞬時に\(V_C\)の出力となります。
回路への落とし込み(ネット衝突検出)
ネットへの衝突条件はボールの位置が0付近かつ、ボールがネットの高さ以下です。\(Y\)方向の判定と\(X\)方向の判定を結合する必要があります。次の回路はネット衝突の判定回路です。
考えに間違いがなければ、追加で1MΩの抵抗が必要です。
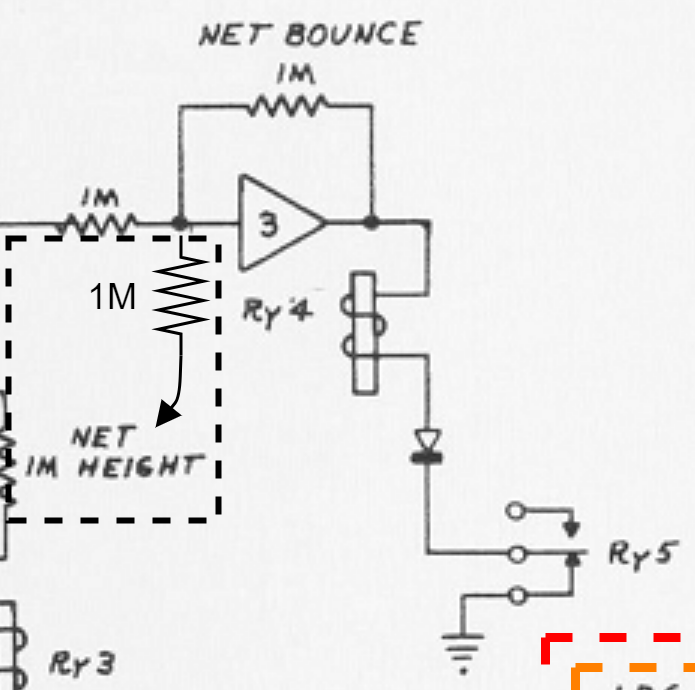
RY4がONになるとネット衝突が検出されネットバウンド回路が動作します。RY4がONになるためには、ダイオードがついているのでアンプ3の出力が正出力である必要があります。さらに、RY5もOFFになる必要があります。まずは、アンプ3が正出力となる条件について探ります。
アンプ3が正出力となる条件は加算回路が基本なっています。ネットの高さを表す電圧\(V_{yn}\)を-1倍し\(-V_{yn}\)加算回路に入力します。ボールの位置を表す電圧\(V_y\)がネットより低くなると正出力になります。アンプ3の出力電圧を表す式は次式です。
$$V_{out}=-(V_y + -V_{yn})$$
上記の式から\(V_{yn} + -V_y > 0\)すなわち、
$$V_{yn} > V_y$$
次にRy5がOFFなる条件ですが、前回説明した通りです。ボールが中心付近になるとOFFとなります。
次回につづきます。

コメント