はじめに
タイトルのまんまです。555で発振回路を作る必要があったので、小ネタです。
555のむ安定マルチの発振周波数を計算します。といっても、解説サイトはいくらでもあります。
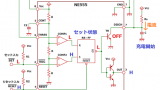
応用回路は腐るほどありますが、代表的な発進回路はこんな感じ。

コンデンサCの充放電を繰り返すことで、矩形波を出力します。発振周波数は次式です。
\[ f = \frac{1.44}{(R_1 + 2R_2)C}\]
CTRL端子を利用
さて、CTRL端子を使わなけば上記の式でよいのですが、発振周波数をCTRL端子から調整した場合の式を導出してみます。内部回路は次のようになっています。
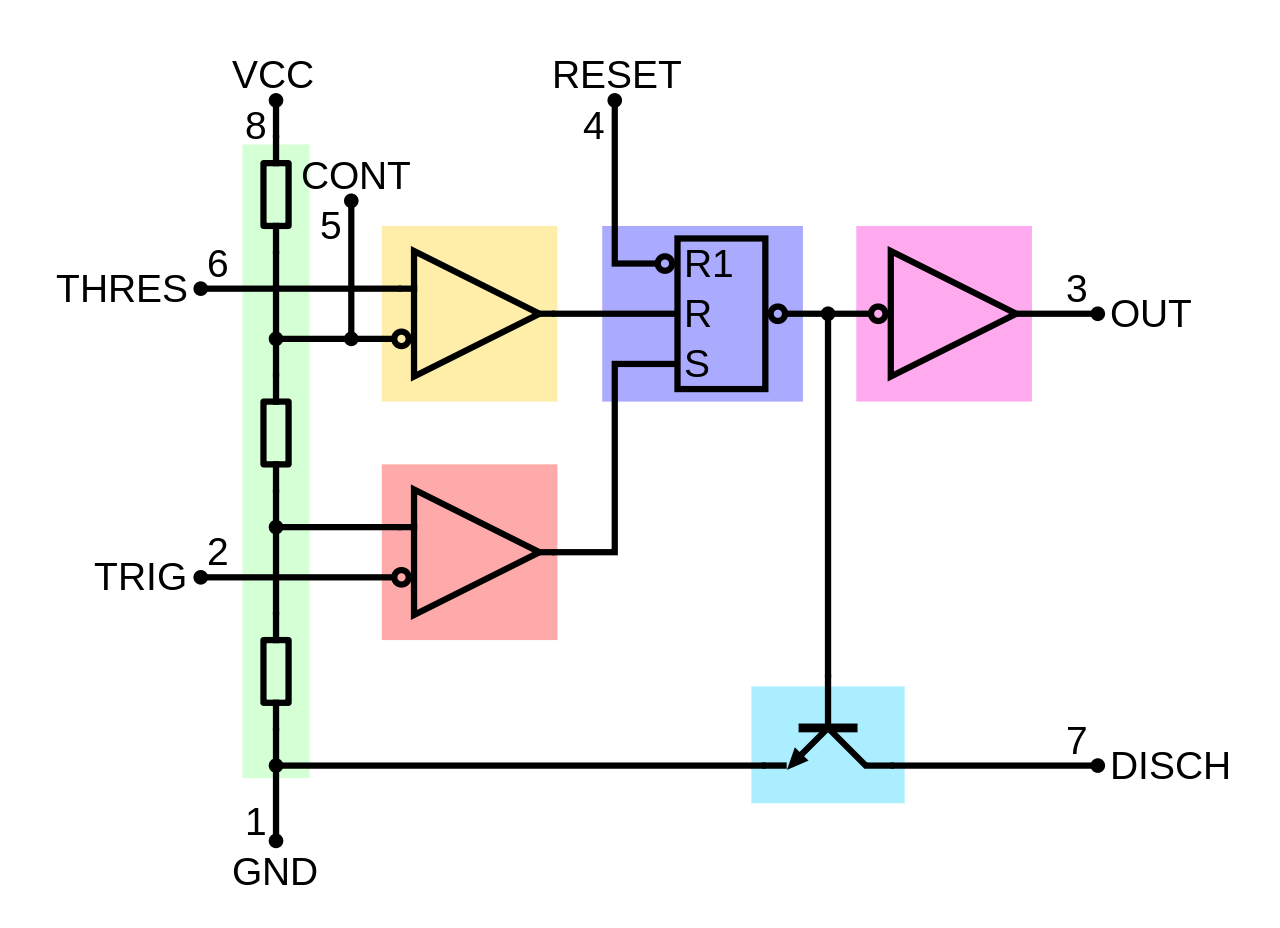
コントロール端子の電圧を\(V_c\), 電源電圧を\(V_{cc}\)とします。赤のコンパレータに入力される電圧は常に\(\frac{V_c}{2}\)となります。このことから、出力はHIGHとなる時間を\(T_H\)とすれば、コンデンサの電圧が\(\frac{V_c}{2}\)から\(V_c\)に充電されるまでには次の関係式が成立します。
\[ \frac{V_c}{2} + \left( V_{cc}-\frac{V_c}{2} \right) \left( 1-e^{-\frac{T_H}{(R_1+R_2)C}} \right) = V_c\]
\[ e^{-\frac{T_H}{(R_1+R_2)C}} = 2\frac{V_{cc}-V_c }{2V_{cc}-V_c } \]
\[ -\frac{T_H}{(R_1+R_2)C} =\ln \left( 2\frac{V_{cc}-V_c }{2V_{cc}-V_c } \right) \]
\[ T_H = (R_1+R_2)C \left[ \ln \left( \frac{1}{2} \right) + \ln \left( \frac{2V_{cc}-V_c}{V_{cc}-V_c} \right) \right] \]
一方、LOWとなる時間を\(T_L\)とすれば、コンデンサの電圧が\(V_c\)から\(\frac{V_c}{2}\)に放電されるまでには次の関係式が成立します。
\[ V_c e^{-\frac{T_L}{R_2C}}= \frac{V_c}{2}\]
したがって、\(T_L \)を求めると、
\[T_L = R_2C\ln (2) \]
コントロール電圧\(V_c\)と無関係になります。発振周波数\(f=\frac{1}{T_H+T_L}\)ですから、
\[ f=\frac{1}{T_H+T_L} = \frac{1}{(R_1+R_2)C \left[ \ln \left( \frac{1}{2} \right) + \ln \left( \frac{2V_{cc}-V_c}{V_{cc}-V_c} \right) \right] + R_2C\ln (2) } \]
うーん 結構複雑な式になってしまった。グラフにするとこんな感じ。NE555Pで実験しました。
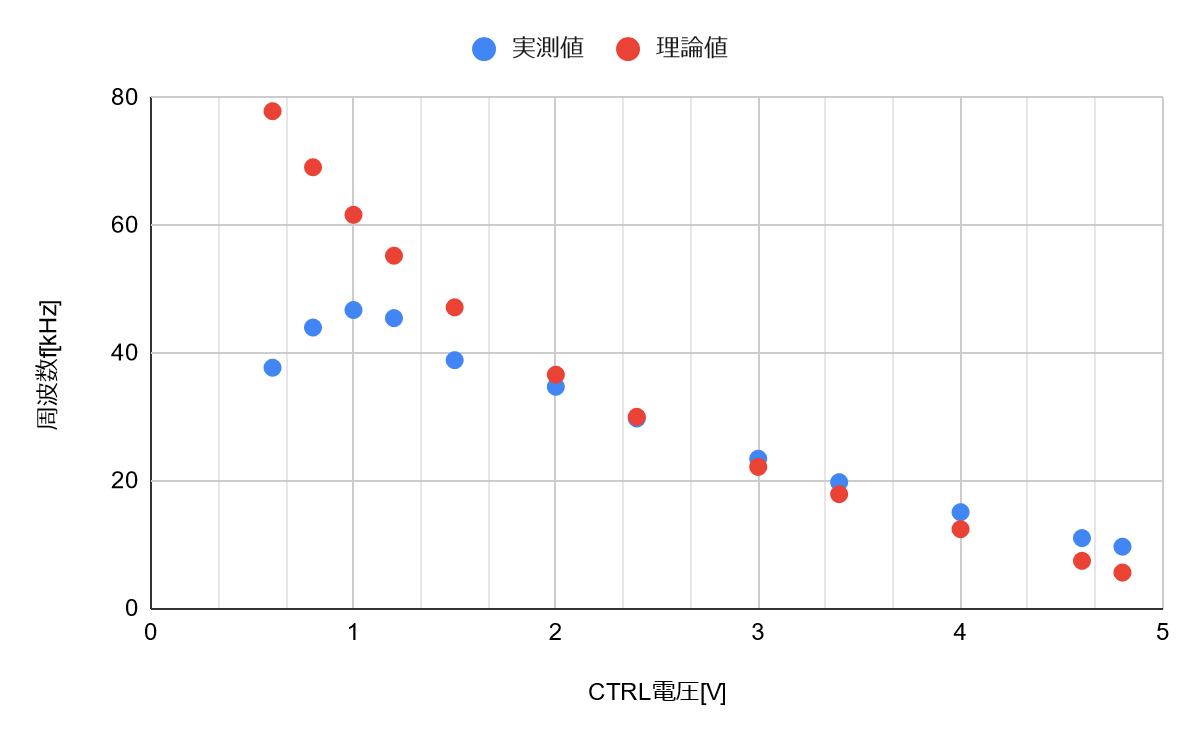
C=2200pF, R1=24kΩ, R2=5600Ωとしました。1V以下はかなりずれます。内部のコンパレータの応答が間に合わないと思われます。
たぶん、式はあってるのかな?


コメント