回路図(1)
回路を5グループに分割し、読み解いていきます。
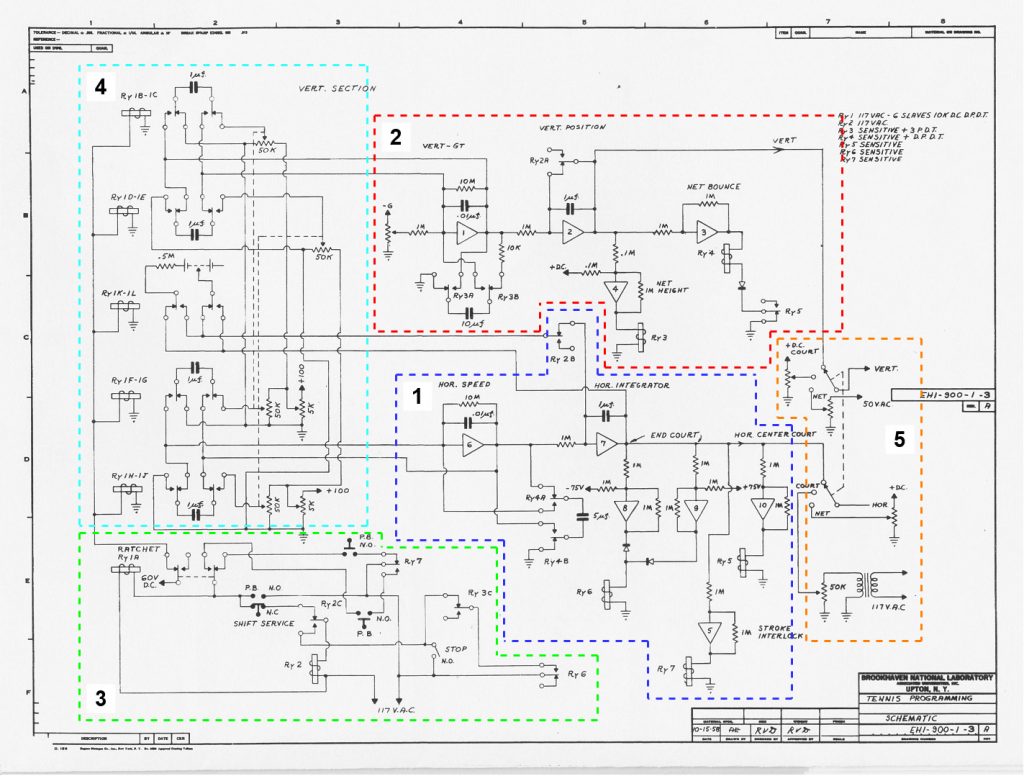
今回は水平方向の運動を計算する回路です。(1)の青の部分です。まずは理論式を確認し、そのあとに回路への落とし込みを考えます。
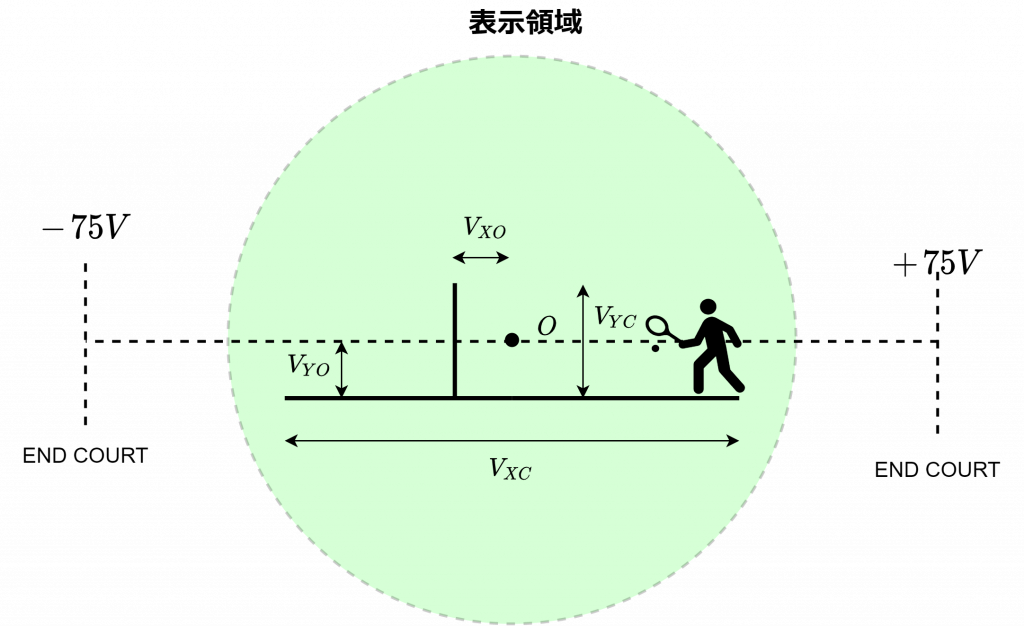
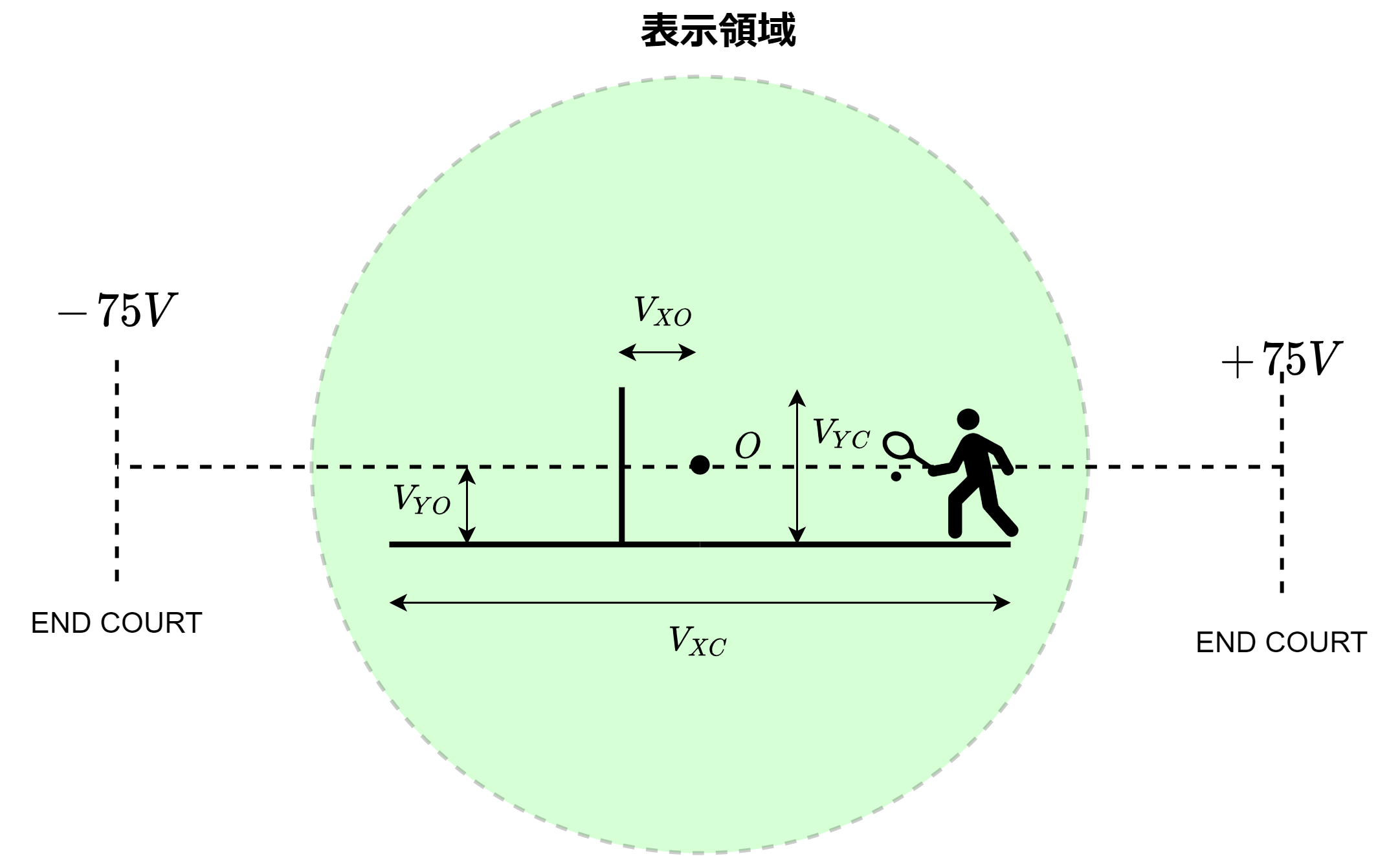
ざっくり、表示領域との関係はこんな感じになってます。\(V_{XO}, V_{XC}, V_{YO}, V_{YC}\)はそれぞれ、ネットの\(X\)方向のオフセット位置、コートの\(X\)方向の大きさ、コートの\(Y\)方向のオフセット位置、ネットの\(Y\)方向の大きさです。
ボールの運動\(X\)方向
このゲームのボールは放物線運動をベースにしているので、\(x\)方向の運動方程式は次式となります。
$$m\frac{d^2x}{dt^2}=0$$
\(m\)はボールの質量です。ただの等速直線運動と変わりません。位置に関する積分方程式に変換します。ただし、初速は打ち返す角度を\( \theta \)として\(v_{0x} = v_0 \cos{\theta}\)とします。
$$x = \int_0^{T} v_{0x} \ dt + x_0$$
\( x_0 \)は初期位置です。当たり前ですが、非常にシンプルな式になりましたね。
ちなみに、このように微分方程式を積分方程式変換して計算させるのは数値計算分野における常套手段ですね。一般に積分を解くほうが難しいので、一般解を求めるには向いていません。ですが、数値積分するだけであれば、逐次的に求めることができるため簡単です。1
ネットのバウンド
次にネットでの反発を考えておく必要がありそうです。ネット反発時には\(x\)方向の速度を反転させる必要があります。そこで、衝突直前の速度を\(V_x\), 位置を\(X_0\)とすると衝突以降の運動は次式となります。
$$x^{hit} = -\int_0^{T} \mathrm{sgn}(V_x) \ dt + X_0$$
回路への落とし込み(ボール位置計算)
さて、先ほどの式を回路に落とし込めばよいわけです。式上では積分器は1つでよいことにはなりますが、ネットによる反発を実現する必要があります。そのためには、速度を記憶しておく必要があるわけです。結果として積分器は2個になります。以下が切り出した回路になります。前段が速度保持用、後段が位置計算用積分器です。
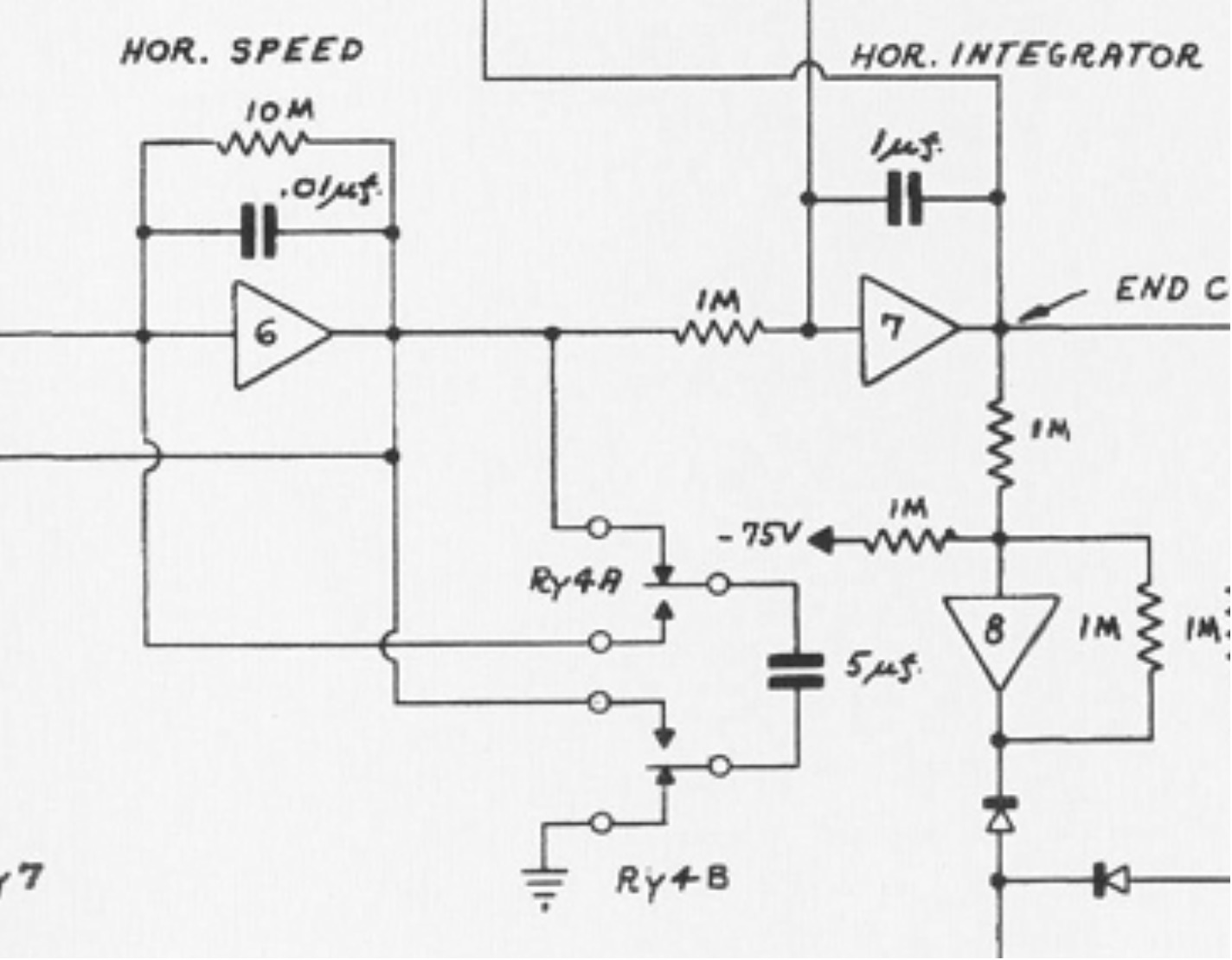
三角記号のものは理想アンプを表しています。入出力間にコンデンサ、入力に抵抗を入れることで次式が成立します。
$$v_{out} = \frac{1}{RC}\int_0^{T} v_{in} \ dt + v_0$$
\(v_0\)はコンデンサの初期電圧です。\(R=1M\Omega\), \(C = 1uF\)とすると、\(\frac{1}{RC}=1\)となり、後段は単純な積分器とみなすことができます。
さて、前段はどうでしょうか?\(10M\Omega\)は一旦無視すると、Rは解放していると考えらえるので\(R=\infty\)とみなせそうです。
$$v_{out} = \frac{1}{RC}\int_0^{T} v_{in} \ dt + v_0 = \frac{1}{\infty}\int_0^{T} v_{in} \ dt + v_0 = v_0$$
すると、初期電圧を常時出力することになります。すなわち、電圧保持回路として動作していると考えれます。(アナログメモリとして考えていいはずです。)後段では積分器としてのみ動作するので、初期電圧\(v_0\)を積分することになります。ここで、初期電圧\(v_0\)を初速\(v_{0x}\)としてみなせばボールの位置を計算していることになります。
これで、ボールの水平方向の弾道計算についてはわかりました。
回路への落とし込み(ネットのバウンド)
5uFのコンデンサは現在の速度を常に保持しておくコンデンサです。ネット衝突時にはリレーにより直接切り替え、前段にあるコンデンサの充放電を急速に行います。前段のコンデンサ容量は1uFですから、速度保持用のコンデンサ5uFのほうがはるかに電圧が支配的になります。また、このとき電圧の極性が反転するように充放電されます。これによって、ネットでのバウンドが実現されます。詳しくは第4回で説明しましょう。
回路への落とし込み(ボールの位置判定)
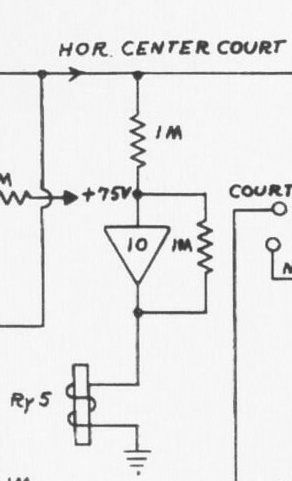
次にボールがコートの外に外れてしまったかどうかを判定する必要があります。先ほどの座標系によると、コートの端は+75V, -75Vになります。ということは水平方向の電圧+75V以上もしくは-75V以下になったことを調べればよさそうです。それを実現したのがこの回路になります。
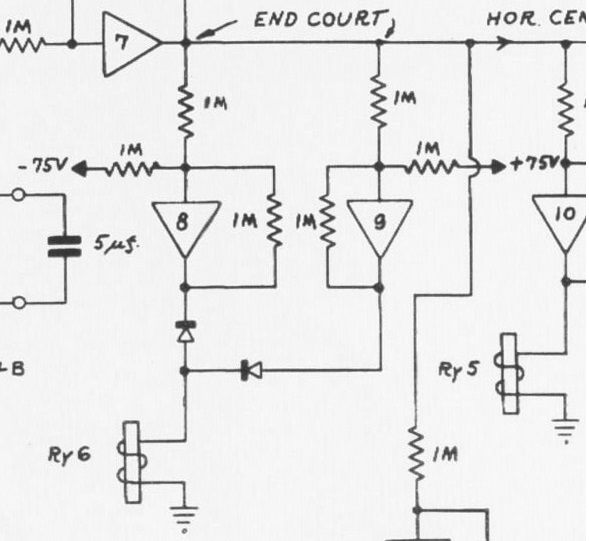
この回路の出力電圧\(V_{out}\)は、ボールの位置を表す電圧を\(V_X\), 理想アンプとして考えれば次式となります。
\[V_{out} = |V_x – 75| \text{step}(V_X – 75) + |-V_x – 75|\text{step}(-V_X – 75)\]
出力にダイオードがついています。これによって、ボールの位置が-75V以下となると8番のアンプ出力が負電圧となり、リレーの電流を引っ張ることができます。反対9番のアンプではボールの位置が+75V以上となると、アンプの出力が正電圧となりリレーがONとなります。これによって、リレーのONによってゲームがリセットされます。
回路への落とし込み(ストローク)
さて、テニスの醍醐味の1つにはお互いに打ち返すストロークにあります。そのためには、ボタンを押し続けていても反応しないようにする必要があります。これはインターロック回路に相当します。ロックの解除条件はネットを超えた瞬間と考えればよいので、次の回路によって判定します。ボールの位置(電圧)が0付近のときのみ、リレーがOFFします。
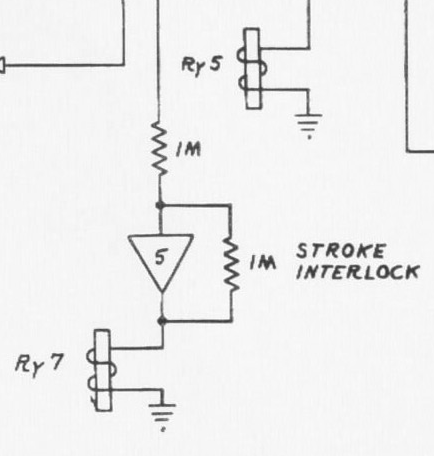
これによって、インターロック(ストローク)が実現できます。
ネット衝突検出(回路への落とし込み)
ボールがネットに衝突する条件は\(X, Y\)両方が影響します。\(X\)条件は0V付近であることが必要です。これは、先ほどのストローク回路と同じになります。
\(Y\)条件は垂直回路の説明のときに行います。
次回に続きます。

コメント