ATAN
アークタンジェントの計算が必要になったので、計算方法について自分なりの理解メモを残しておきます。
直交するセンサの値を検出できるとき、よく角度が必要になることが多いです。意外とATANの計算は面倒なので、MCUで計算する方法を簡単にまとめておきます。速度、精度の両方を追求しようとすると結構やっかいです。多くの場合、速度と精度のどちらか一方でよい場合が多いと思います。
- 内蔵機能を使う
- 近似を使う
- ライブラリを使う
- CORDIC
- あきらめる。
内蔵機能
最近のマイコンであれば、ルネサスTFU機能とかがあるので、それを使うのが精度、速度面両方から考えても一番かと思います。ある程度、処理能力のあるMCUでないと実現できないので、今回はパスです。
近似する
ATANの0付近では\(y=tan^{-1} x = x\)として近似できます。0付近でしか使わない、精度が問題にならない場合は最も合理的な手法ですね。もう少し精度を求めるのであれば、マクローリン展開で3項まで計算するとだいぶよくなりますが、乗除算が必要になるので、チープなMCUでは難点があります。今回はもう少し、精度を求めてみます。(他の分母多項式を使った近似もあるようです。)
ライブラリを使う。
math.hのライブラリを使うことでも計算できます。処理的にはほぼ全て 多項式近似(範囲分割+係数テーブル)で実装されているそうです。GPT調べですが、
CORDIC
これが、今使おうとしている方法です。結構面白い方法でして賢い方法です。テーブル参照とベクトル回転を組み合わせています。反復回数を調整すれば精度も変えられるので面白ですね。方法的にはAD変換の逐次変換と似ているところが面白いです。よく、図形を用いて説明されますが、式だけで説明してみます。
今、求めたいベクトルの座標を\(x, y\), 角度を\(\theta\)とします。アルゴリズムとしては、回転角度を小さくしながら、ベクトルを\(x\)軸に一致させる方向に回転させます。ベクトルが第一、第二象限にあるときは、時計回り、第三、第四象限にあるときは反時計回りに回転させます。このとき、回転角度は反復ごとに小さくします。(通常は\(\frac{\pi}{4}\)を初期角度として、回転角度を半分にながら、回転させます。)
すると、上記の動作を反復させることでベクトルを\(x\)軸に一致させます。このとき、符号を含めた回転角度\(\phi_i\)の総和を計算することで、ベクトルの角度\(\theta\)が求まります。
\[ \theta = \sum_i \phi_i \]
アルゴリズムとしては簡単なのですが、そのまま実装するとベクトル回転のために\(\sin, \cos\)の計算が必要になるのでやっかいです。ですが、アルゴリズムを考えると、あくまで必要なのは角度なので、ベクトルを回転させても\(x, y\)のスケールは変わってもよいわけです。すると、計算を単純化できます。
さて、計算を単純化させるために回転行列を考えてみます。ベクトルの座標を\(x, y\)として、角度を\(\phi\)だけ回転し、ベクトルを\(x’, y’\)に移動させる回転行列は次のように計算できます。
\[ X = \begin{bmatrix} x \\ y \end{bmatrix} \\ X’ = \begin{bmatrix}
x’ \\
y’
\end{bmatrix} = \begin{bmatrix}
\cos{\phi} && -\sin{\phi} \\
\sin{\phi} && \cos{\phi} \end{bmatrix} X \]
まずは、1変数に落とし込みたいので、\(\cos{\phi}\)でくくりだします。
\[ X’ = \begin{bmatrix}
x’ \\
y’
\end{bmatrix} = \cos{\phi} \begin{bmatrix}
1 && -\tan{\phi} \\
\tan{\phi} && 1 \end{bmatrix} X \]
行列に\(\tan{\phi}\)が残っていますが、
\[ \begin{bmatrix}
x’ \\
y’
\end{bmatrix} = X \cos{\phi} + \cos{\phi} \begin{bmatrix}
0 && -\tan{\phi} \\
\tan{\phi} && 0 \end{bmatrix} X \]
このように考えます。適当なスケーリング係数\(K>0\)をかけても、ベクトルの角度は変わらないので、スケーリング後のベクトル座標を\(x”, y”\)とすると、\(\cos{\phi}\)を含めて、
\[ \bar{X} = (\cos{\phi}) X \\ \begin{bmatrix}
x” \\
y”
\end{bmatrix} = \bar{X} + \begin{bmatrix}
0 && -K\tan{\phi} \\
K\tan{\phi} && 0 \end{bmatrix} \bar{X} \]
となります。次に反復させることを考えます。
反復させるごとに回転角の絶対値は小さくしなければ、ベクトルは\(x\)軸に一致しないので、以下の条件設定が必要です。反復回数を\(i\)として、
\[ 0 < |\phi_i| < |\phi_{i-1}| \]
とする必要があります。(インデックスは1から)今回は初期角度を\(\frac{\pi}{4}\)として、反復ごとに角度を1/2にします。ただし、回転方向は\(x\)軸に近づく方向に回転させる必要があるので、符号関数を\(sgn\)として、
\[ \phi_i = -sgn(\phi_{i-1}) \frac{\phi_{i-1}}{2} \]
となります。スケーリング係数\(K_i>0\)は自由に選べますので、\(tan\)の計算が発生しないように選びます。\(tan\)は\(\phi_i\)に応じて正負に切り替わるので、注意が必要です。
\[ K_i= \frac{ 2^{-i}}{|\tan{\phi_{i-1}}|}\]
として選べば、符号関数を\(s=sgn\)、\(\phi→\phi_{i-1}\)にして先ほどの式は以下のように計算しても回転を実現できます。
\[ -K_i\tan{\phi_{i-1}}=-\frac{ 2^{-i}}{|\tan{\phi_{i-1}}|}\tan{\phi_{i-1}}=s(\phi_{i-1})2^{-i} \]
\[ \begin{bmatrix}
x_{i} \\
y_{i}
\end{bmatrix} = \bar{X} + \begin{bmatrix}
0 && s(\phi_{i-1})2^{-i} \\
-s(\phi_{i-1})2^{-i} && 0 \end{bmatrix} \bar{X} \]
\(-\pi <\phi_i < \pi\)なので、符号は\(y_{i-1}\)で判別します。\[ \begin{bmatrix}
x_{i} \\
y_{i}
\end{bmatrix} = \bar{X} + \begin{bmatrix}
0 && s(y_{i-1})2^{-i} \\
-s(y_{i-1})2^{-i} && 0 \end{bmatrix} \bar{X} \]
反復させることでベクトルの回転を実現できそうです。ここで、\(2^{-i}\)はiビットのビットシフトで実現できるので非力なMCUでも実現できます。最終的な角度は、
\[ \theta = \sum_{i=1} -s(y_i) (\frac{\pi}{4}) 2^{-i} \]
として、求まります。
確認してみる。初期値として、\(X_0=0.6, Y_0=0.8\)としました。
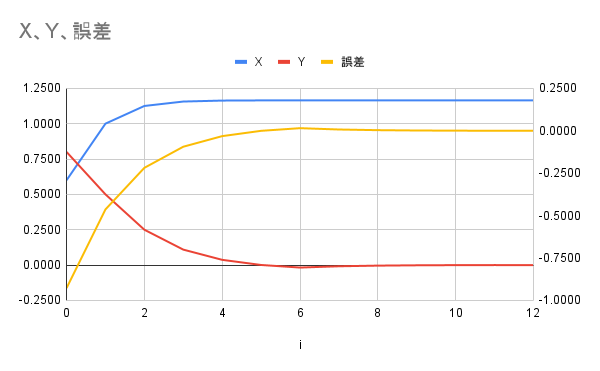
このように、Y=0となっているので、X軸に収束していることがわかります。このとき、角度は0.9274radであり、真値の0.927295radと3桁以上の精度があります。
細かいところでは、初期値の選択や回転角度の自由度がありますが今回は考えてないです。
あきらめる。
そもそもアークタンジェントが必要なのかというところですね。
テーブル参照でそれっぽくもできるかもですね。


コメント