CRTに必要な偏向回路をつくります。
さて、CRTの偏向回路を駆動するのにのこぎり波が必要です。
矩形波状の同期波形から振幅を一定に保つのこぎり波っぽい波形を生成します。回路はDeboo積分回路を基本に設計してみました。
Deboo積分回路は単電源でも使える便利な積分回路の一種です。コンデンサが帰還回路の外部にあるので、リセットがしやすく今回使ってみました。
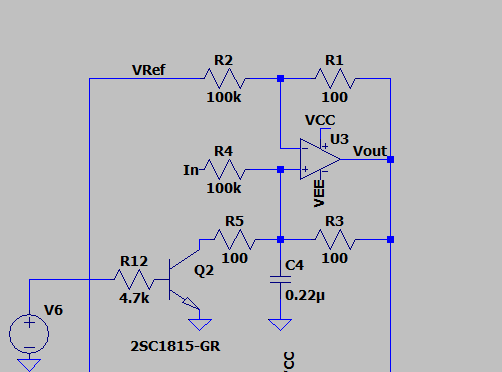
出力と入力の関係性を求めてみます。バーチャルショートの関係から、
非反転入力端子と反転入力端子の出力は同じになります。したがって、反転入力端子の電圧は、
\[V_{-} = \frac{R_1 V_{REF} + R_2 V_{out}}{R_1 + R_2}\]
となります。一方、非反転入力端子の電圧はコンデンサに出力からの電流と入力からの電流が合算されると考えて、
\[V_+ = \frac{1}{C}\int_0^T \frac{V_{out} – V_c}{R_3} + \frac{V_{IN} – V_c}{R_4} dt\]
ラプラス変換すると、
\[ \left ( sC + \frac{R_3 + R_4}{R_3 R_4}\right ) V_+ = \frac{R_4 V_{out} + R_3 V_{IN}}{R_3 + R_4}\]
\[ V_+ = \frac{R_4 V_{out} + R_3 V_{IN}}{sCR_3 R_4 + R_3 + R_4} \]
\( V_+ = V_-\)より、
\[ V_{out} = \frac{R_3V_{IN}(R_1+R_2)-R_1V_{REF}(sCR_3R_4+R_3+R_4)}{R_2(sCR_3R_4+R_3R_4)-R_4(R_1+R_2)} \]
となります。\(s=0\)以外の極があると、出力に指数関数を含むことになるで、\(R=R_2R_3=R_1R_4\)として選ぶと、出力は
\[ V_{out} = \frac{(R+R_1R_3)(V_{IN}-V_{REF})-scRR_3V_{REF}}{sCR_3R_4}\]
このように、単純な積分器として動作することがわかりますが、出力にオフセットが残ってしまうので、\(R_4\gg R_3\gg 1\)として選べば、近似的に
\[ V_{out} = \frac{(R+R_1R_3)(V_{IN}-V_{REF})}{scRR_4} = \frac{R_1}{sCR_2R_4}(V_{IN}-V_{REF})\]
となります。したがって、積分ゲイン\(G=\frac{R_1}{CR_2R_4}\)となります。\(R_1=R_3=100, R_2=R_4=100k, C=0.22\mu \)として選ぶと、
\[ G=\frac{1}{22}= 0.0454\]
となります。
ピークフィードバック回路をつけたす
コンデンサの放電用トランジスタをつければ、のこぎりは変換は可能ですが、もう少し凝ってみます。入力パルスの周波数、dutyが変化しても振幅を一定に保てるようにAGC?的なフィードバックを施します。
のこぎり波の振幅と目標値の差分を増幅して積分回路に入力することで実現することにします。
あんまりOPAMPを使う数を増やしたくないので、ピーク検出は簡易的な半波整流回路を使うことにしました。あとは目標値とピーク検出値を差動増幅回路に入力するだけです。
こんな回路になりました。
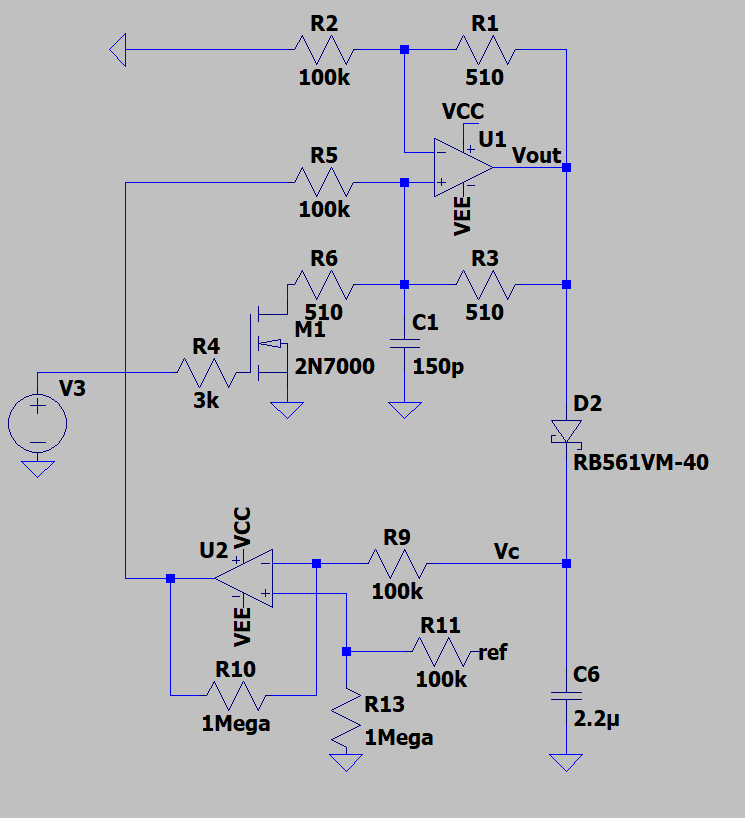
OPAMPには単電源のJNM13404Dを使いました。
回路はこんな感じ。差動増幅のゲインはカットアンドトライです。

適当に15kHz前後の信号を入力して、みたところ次のようになりました。
普通、同期信号は負論理なので反転させる必要があります。
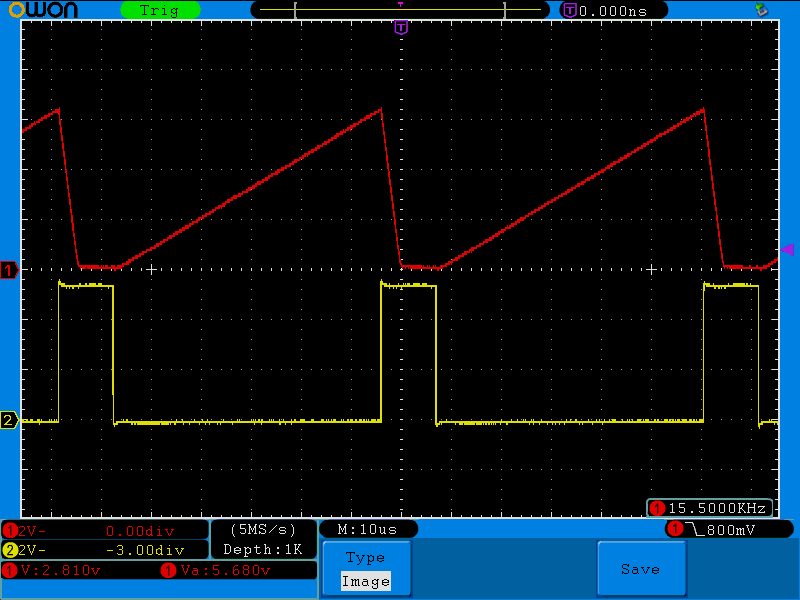
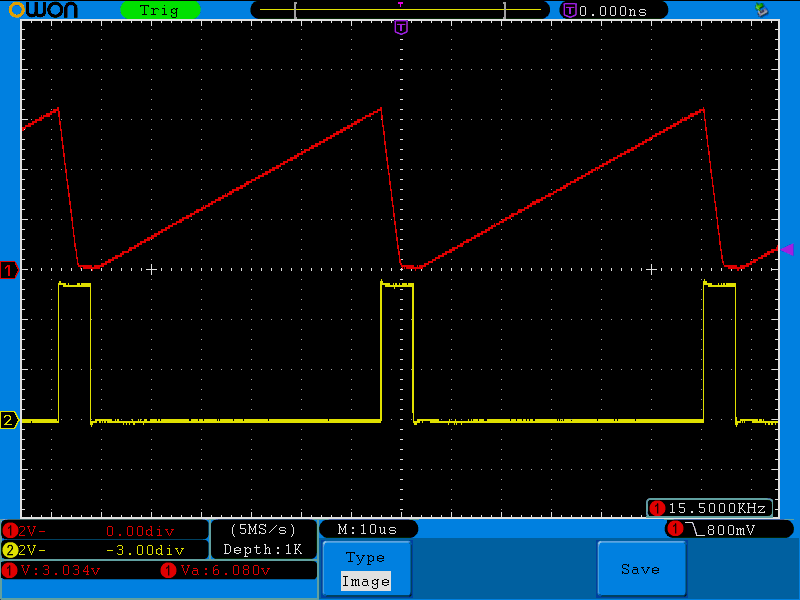
振幅の目標値を変えてもパルス幅に追従しています。
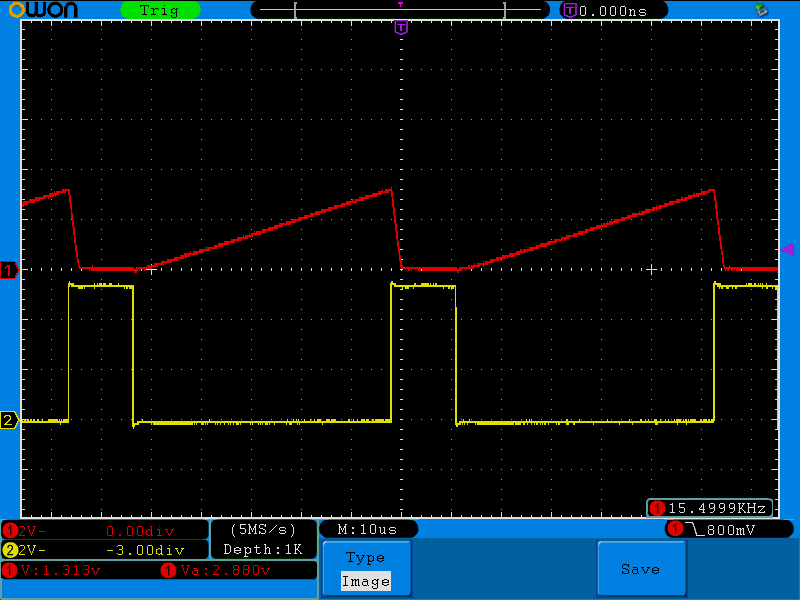
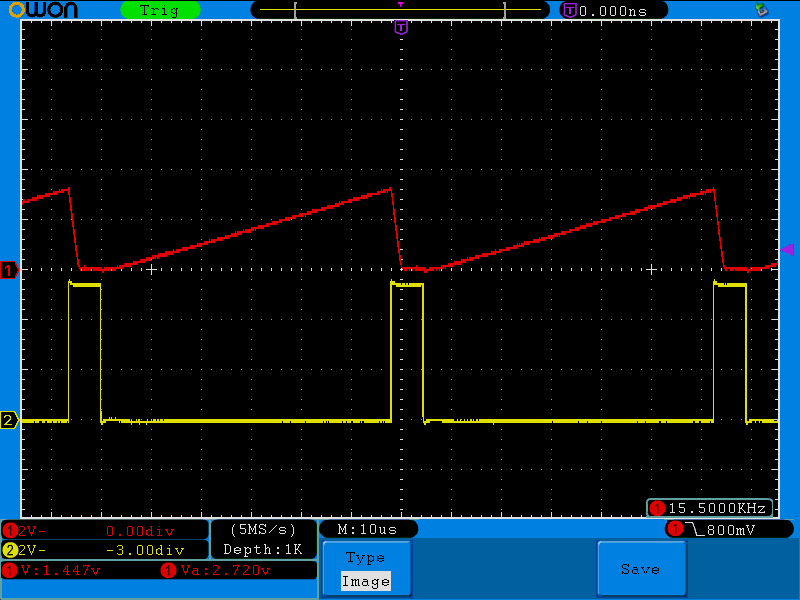
いい感じ?
あとは、オフセット調整用のOPAMPを接続すれば偏向コイルに与える基準信号がつくれそうです。

コメント